Publications
2022
-
-
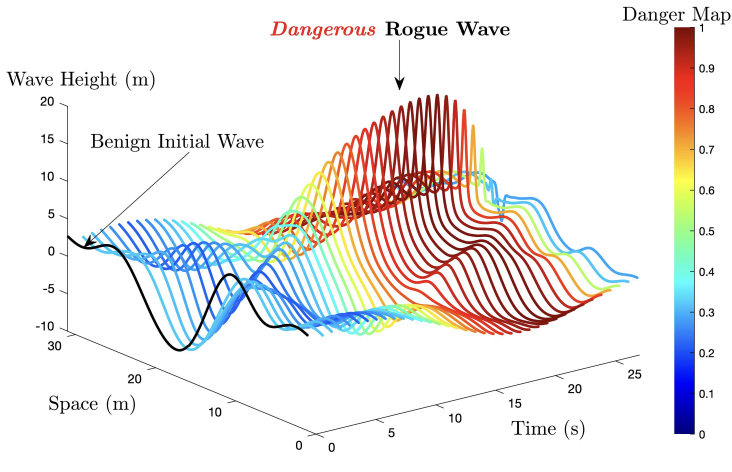
Discovering and forecasting extreme events via active learning in neural operators
E. Pickering, S. Guth, G. Em Karniadakis, T.P. Sapsis
Nature Compuational Science (2022)
BIB ABSTRACT
Extreme events in society and nature, such as pandemic spikes, rogue waves or structural failures, can have catastrophic consequences. Characterizing extremes is difficult, as they occur rarely, arise from seemingly benign conditions, and belong to complex and often unknown infinite-dimensional systems. Such challenges render attempts at characterizing them moot. We address each of these difficulties by combining output-weighted training schemes in Bayesian experimental design (BED) with an ensemble of deep neural operators. This model-agnostic framework pairs a BED scheme that actively selects data for quantifying extreme events with an ensemble of deep neural operators that approximate infinite-dimensional nonlinear operators. We show that not only does this framework outperform Gaussian processes, but that (1) shallow ensembles of just two members perform best; (2) extremes are uncovered regardless of the state of the initial data (that is, with or without extremes); (3) our method eliminates ‘double-descent’ phenomena; (4) the use of batches of suboptimal acquisition samples compared to step-by-step global optima does not hinder BED performance; and (5) Monte Carlo acquisition outperforms standard optimizers in high dimensions. Together, these conclusions form a scalable artificial intelligence (AI)-assisted experimental infrastructure that can efficiently infer and pinpoint critical situations across many domains, from physical to societal systems.
-
-
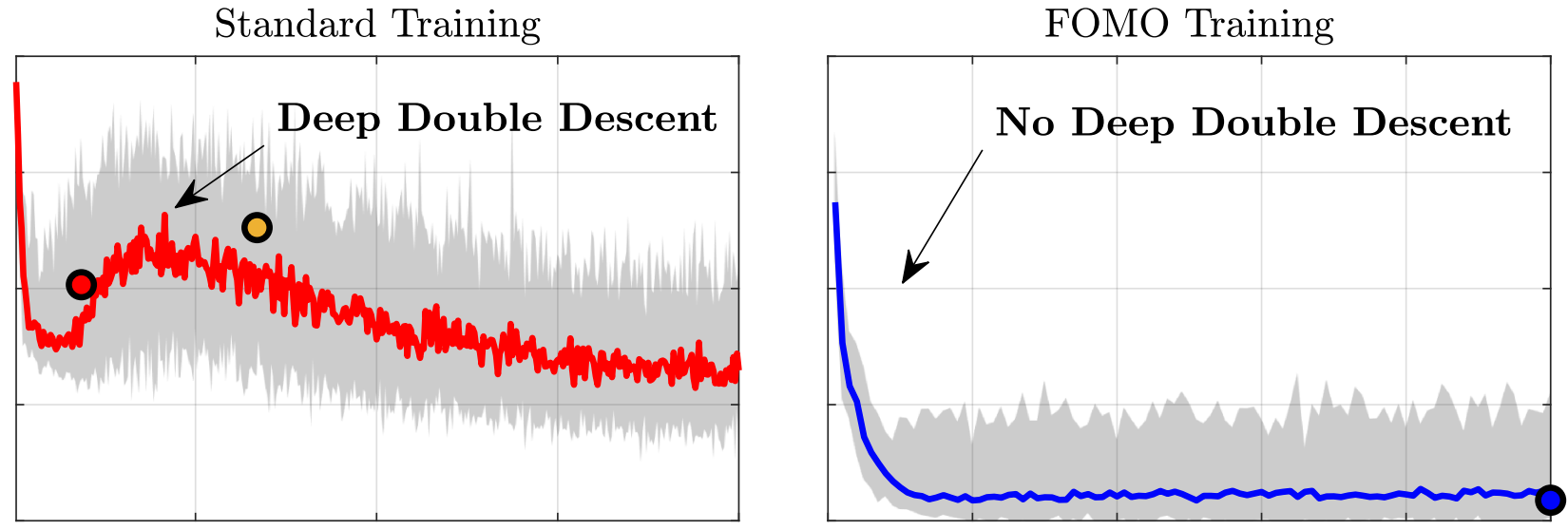
Information FOMO, The unhealthy fear of missing out on information. A method for removing misleading data for healthier models
E. Pickering, T.P. Sapsis
Submitted (2022)
BIB ABSTRACT
Misleading or unnecessary data can have out-sized impacts on the health or accuracy of Machine Learning (ML) models. We present a Bayesian sequential selection method, akin to Bayesian experimental design, that identifies critically important information within a dataset, while ignoring data that is either misleading or brings unnecessary complexity to the surrogate model of choice. Specifically, our method eliminates the phenomena of double descent, where more data leads to worse performance. Our approach has two key features. First, the selection algorithm dynamically couples the chosen model and data. Data is chosen based on its merits towards improving the selected model, rather than being compared strictly against other data. Second, a natural convergence of the method removes the need for dividing the data into training, testing, and validation sets. Instead, the selection metric inherently assesses testing and validation error through global statistics of the model. This ensures that key information is never wasted in testing or validation. The method is applied using both Gaussian process regression and deep neural network surrogate models.
-

-
Structure and Distribution Metric for Quantifying the Quality of Uncertainty-Assessing Gaussian Processes, Deep Neural Nets, and Deep Neural Operators for Regression
E. Pickering, T.P. Sapsis
Submitted (2022)
BIB ABSTRACT
We propose two bounded comparison metrics that may be implemented to arbitrary dimension in regression tasks. One quantifies the structure of uncertainty and the other quantifies the distribution of uncertainty. The structure metric assesses the similarity in shape and location of uncertainty with the true error, while the distribution metric quantifies the supported magnitudes between the two. We apply these metrics to Gaussian Processes (GPs), Ensemble Deep Neural Nets (DNNs), and Ensemble Deep Neural Operators (DNOs) on high-dimensional and nonlinear test cases. We find that comparing a model's uncertainty estimates with the model's squared error provides a compelling ground truth assessment. We also observe that both DNNs and DNOs, especially when compared to GPs, provide encouraging metric values in high dimensions with either sparse or plentiful data.
-

-
Efficient global resolvent analysis via the one-way Navier-Stokes equations
A. Towne, G. Rigas, O. Kamal, E. Pickering, T. Colonius
Journal of Fluid Mechanics, 948, A9 (2022)
BIB ABSTRACT
Resolvent analysis is a powerful tool for modelling and analysing transitional and turbulent flows and, in particular, for approximating coherent flow structures. Despite recent algorithmic advances, computing resolvent modes for flows with more than one inhomogeneous spatial coordinate remains computationally expensive. In this paper we show how efficient and accurate approximations of resolvent modes can be obtained using a well-posed spatial marching method for flows that contain a slowly varying direction, i.e. one in which the mean flow changes gradually. First, we derive a well-posed and convergent one-way equation describing the downstream-travelling waves supported by the linearized Navier–Stokes equations. The method is based on a projection operator that isolates downstream-travelling waves. Integrating these one-way Navier–Stokes (OWNS) equations in the slowly varying direction, which requires significantly less CPU and memory resources than a direct solution of the linearized Navier–Stokes equations, approximates the action of the resolvent operator on a forcing vector. Second, this capability is leveraged to compute approximate resolvent modes using an adjoint-based optimization framework in which the forward and adjoint OWNS equations are marched in the downstream and upstream directions, respectively. This avoids the need to solve direct and adjoint globally discretized equations, therefore bypassing the main computational bottleneck of a typical global resolvent calculation. The method is demonstrated using the examples of a simple acoustics problem, a Mach 1.5 turbulent jet and a Mach 4.5 transitional zero-pressure-gradient flat-plate boundary layer. The optimal OWNS results are validated against corresponding global calculations, and the close agreement demonstrates the near-parabolic nature of these flows.
2021
-

-
Resolvent-based modeling of turbulent jet noise
E. Pickering, A. Towne, P. Jordan, T. Colonius
Journal of the Acoustical Society of America (2021)
BIB ABSTRACT
Resolvent analysis has demonstrated encouraging results for modeling coherent structures in jets when compared against their data-educed counterparts from high-fidelity large-eddy simulations (LES). We formulate resolvent analysis as an acoustic analogy that relates the near-field resolvent forcing to the near- and far-field pressure. We use an LES database of round, isothermal, Mach 0.9 and 1.5 jets to produce an ensemble of realizations for the acoustic field that we project onto a limited set of resolvent modes. In the near-field, we perform projections on a restricted acoustic output domain, r/D=[5,6], while the far-field projections are performed on a Kirchhoff surface comprising a 100-diameter arc centered at the nozzle. This allows the LES realizations to be expressed in the resolvent basis via a data-deduced, low-rank, cross-spectral density matrix. We find that a single resolvent mode reconstructs the most energetic regions of the acoustic field across Strouhal numbers, St=[0−1], and azimuthal wavenumbers, m=[0,2]. Finally, we present a simple function that results in a rank-1 resolvent model agreeing within 2dB of the peak noise for both jets.
-
-
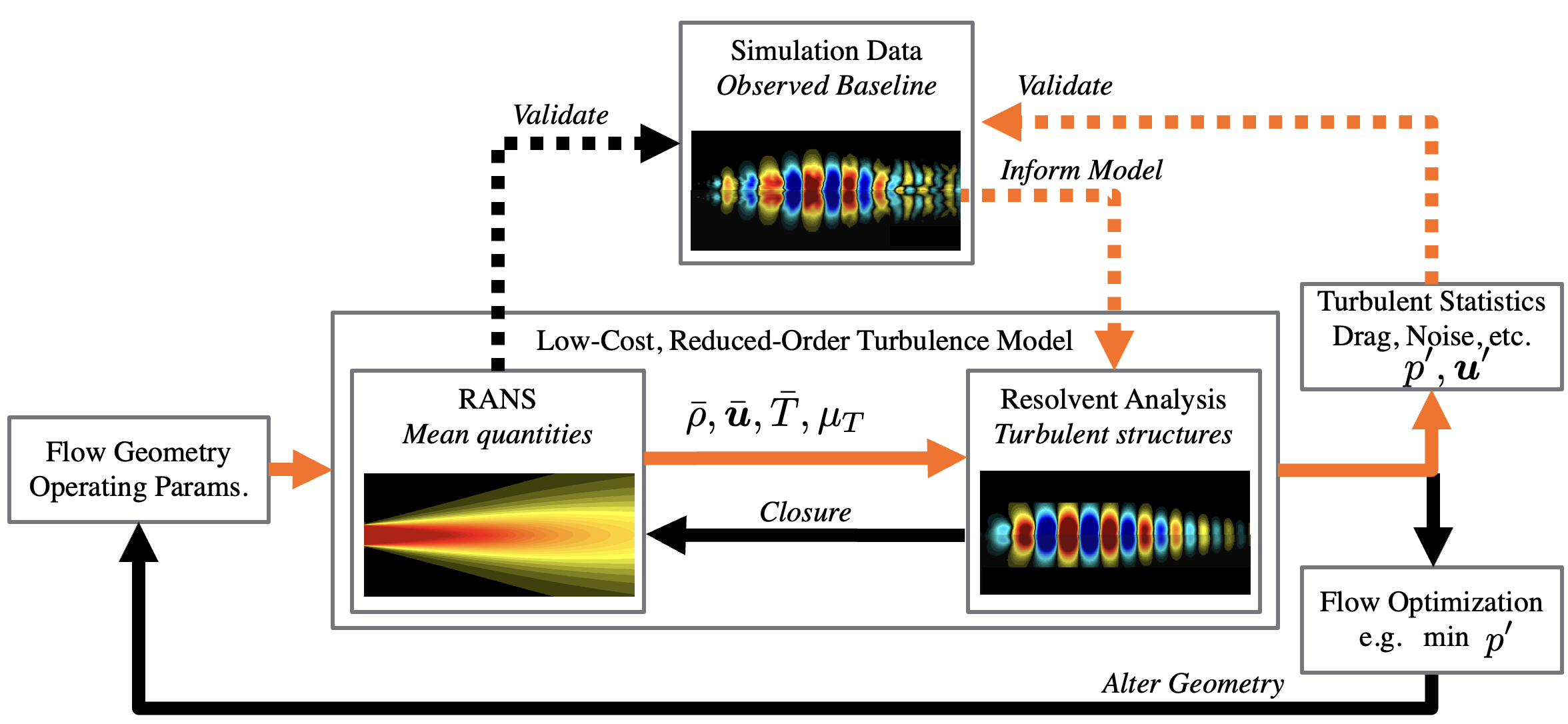
Resolvent modeling of turbulent jets
E. Pickering
Ph.D. Dissertation, California Institute of Technology (2021)
BIB ABSTRACT
Optimal control of turbulent flows requires a detailed prediction of the unsteady, three-dimensional turbulent structures that govern quantities of interest like noise, drag, and mixing efficiency. There is a need for physics-based, reduced-order models of turbulent structure for those cases where direct simulation of the flow would be computationally prohibitive. In this thesis, we explore resolvent analysis as a framework for such models. Based on a linearization about the turbulent mean flow field, the resolvent finds optimal (highest gain) forcing functions that give rise, through linear amplification mechanisms, to energetic coherent structures. The forcing functions represent the nonlinear interactions between the coherent structures as well as with background incoherent turbulence. While the high-gain structures capture many characteristics of the observed turbulent coherent structures in both wall-bounded and free-shear flows, closures for the forcing function are required to make these models predictive and thus utilize them for flow control. In the first part of this thesis, we examine a linear model for the resolvent forcing by adapting the concept of a turbulent (eddy) viscosity from classical Reynolds-Averaged Navier-Stokes (RANS) turbulence modeling. We present a data-driven approach to identify an optimal eddy-viscosity field that best matches the resolvent prediction to the most energetic coherent structure educed via spectral proper orthogonal decomposition (SPOD) of data from high-fidelity simulations. We analyze the specific case of turbulent jets spanning a range of Mach numbers from subsonic to supersonic. We find the optimal eddy-viscosity field to be effective at matching both the shape and energy distribution of structures. More importantly, we find that calibrated eddy-viscosity fields predicted using standard eddy-viscosity models (utilizing only quantities available from RANS) yield results that are close to optimal. We use the resulting resolvent model together with the high-fidelity data to investigate the full spectrum of amplification mechanisms and coherent structures present in turbulent jets. The addition of a turbulence model provides a clear separation between two established mechanisms in turbulent jets (Kelvin-Helmholtz and Orr) and leads to the identification of a third mechanism known as lift-up. Lift-up becomes the dominant mechanism at low-frequency limits for nonzero azimuthal wavenumbers, generating elongated, streaky structures. We find these streaks to be the most energetic structures in the jet, and that their presence has implications for altering the mean flow and controlling noise. Finally, we extend resolvent analysis to that of an acoustic analogy that relates the near-field forcing to the far-field acoustics 100 diameters from the nozzle. We again leverage high-fidelity data to produce an ensemble of realizations of the acoustic field and find that only a few resolvent modes are necessary for reconstruction. Ultimately, we find that a resolvent model based solely upon RANS quantities can reconstruct and predict the peak acoustic field at rank-1 to within 2 decibels for both the supersonic and transonic jets.
-
-
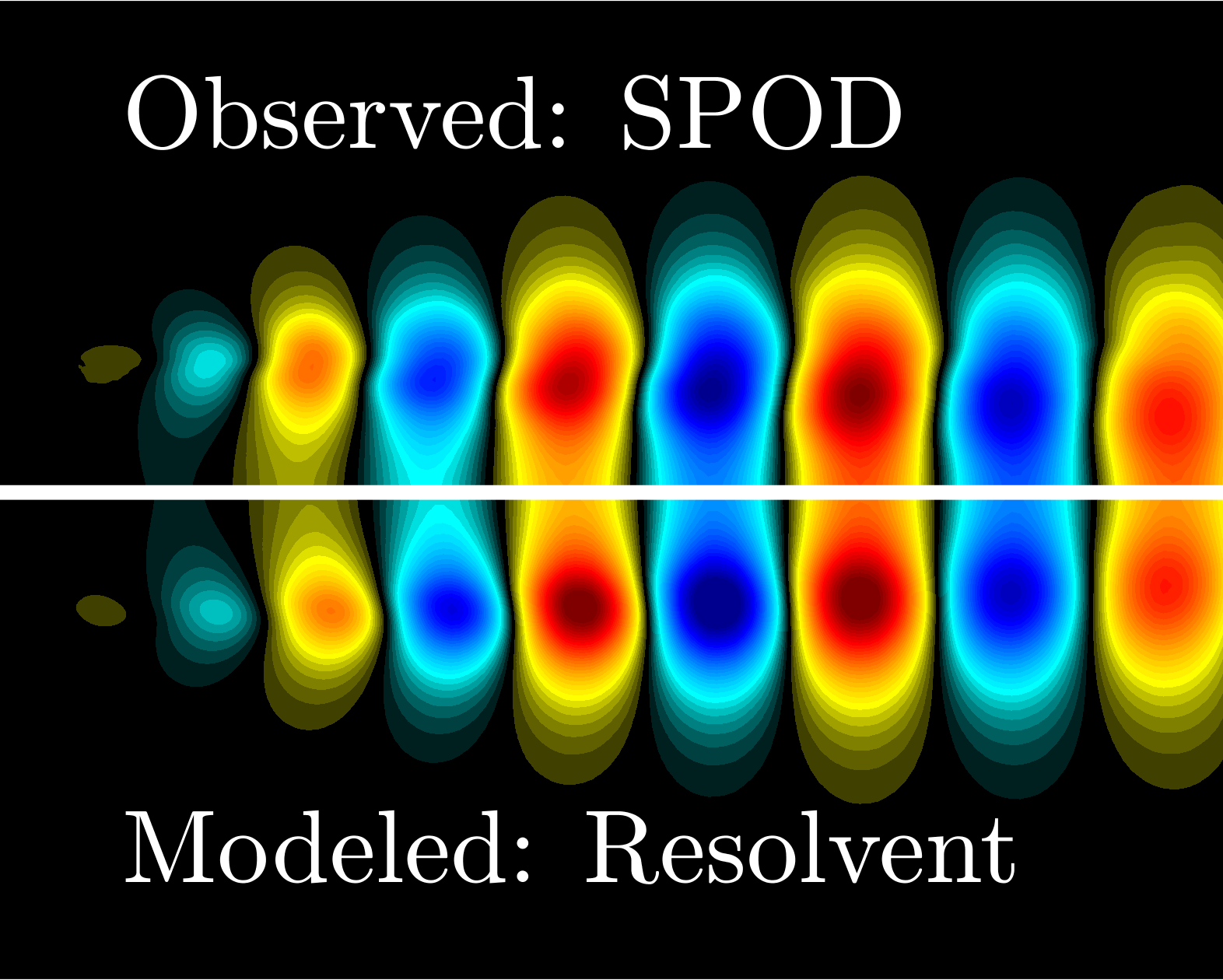
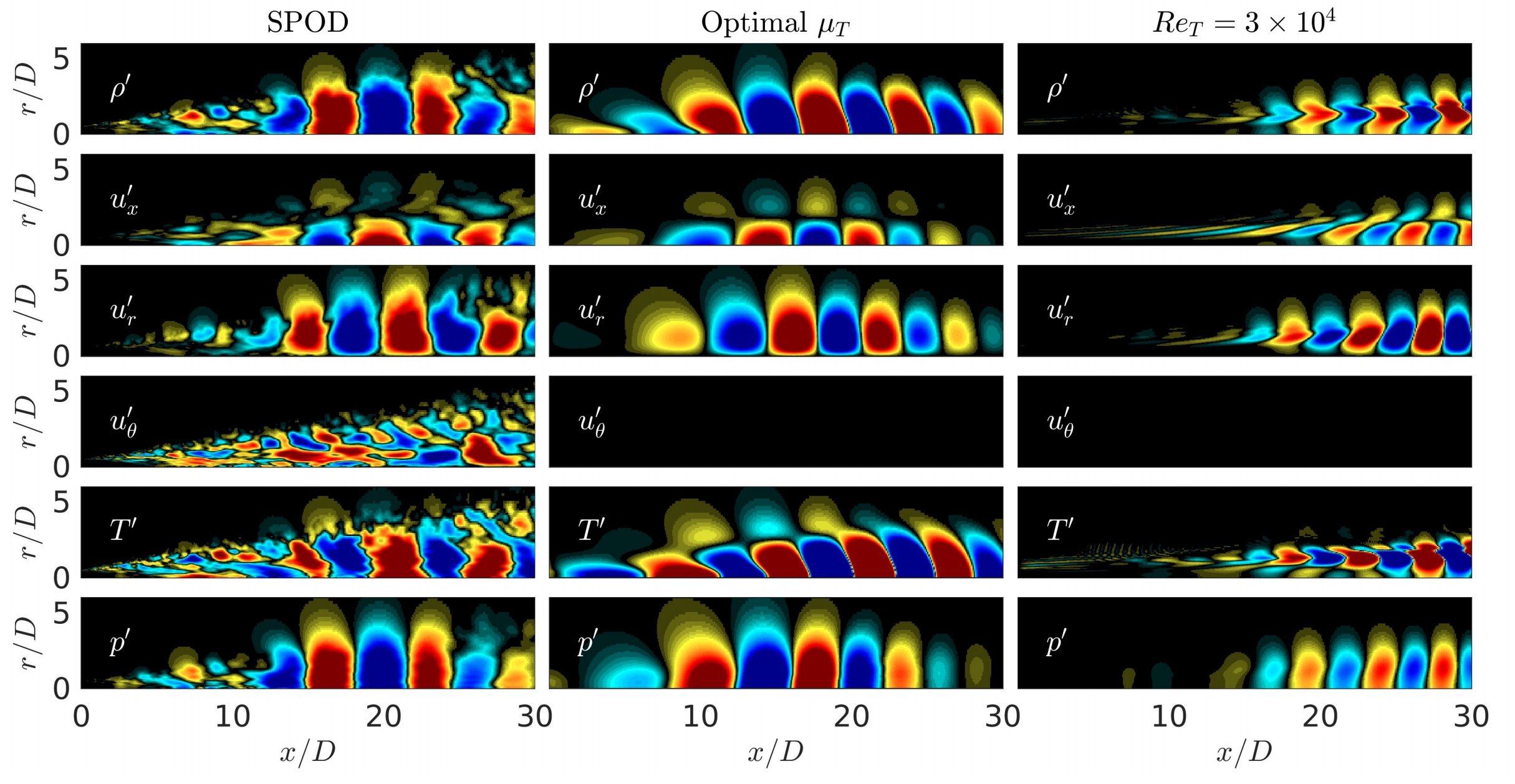
Optimal eddy viscosity for resolvent-based models of coherent structures in turbulent jets
E. Pickering, G. Rigas, O. T. Schmidt, D. Sipp, T. Colonius
Journal of Fluid Mechanics, 917, A29 (2021)
BIB ABSTRACT
Response modes computed via linear resolvent analysis of a turbulent mean-flow field have been shown to qualitatively capture characteristics of the observed turbulent coherent structures in both wall-bounded and free shear flows. To make such resolvent models predictive, the nonlinear forcing term must be closed. Strategies to do so include imposing self-consistent sets of triadic interactions, proposing various source models, or through turbulence modelling. For the latter, several investigators have proposed using the mean-field eddy viscosity acting linearly on the fluctuation field. In this study, a data-driven approach is taken to quantitatively improve linear resolvent models by deducing an optimal eddy-viscosity field that maximizes the projection of the dominant resolvent mode to the energy-optimal coherent structure educed using spectral proper orthogonal decomposition (SPOD) of data from high-fidelity simulations. We use large-eddy simulation databases for round isothermal jets at subsonic, transonic, and supersonic conditions and show that the optimal eddy viscosity substantially improves the agreement between resolvent and SPOD modes, reaching over 90% agreement at those frequencies where the jet exhibits a low-rank response. We then consider a fixed model for the eddy viscosity and show that with the calibration of a single constant, the results are generally close to the optimal one. In particular, the use of a standard Reynolds-Averaged-Navier-Stokes (RANS) eddy-viscosity resolvent model, with a single coefficient, provides substantial agreement between SPOD and resolvent modes for three turbulent jets and across the most energetic wavenumbers and frequencies.
2020
-

-
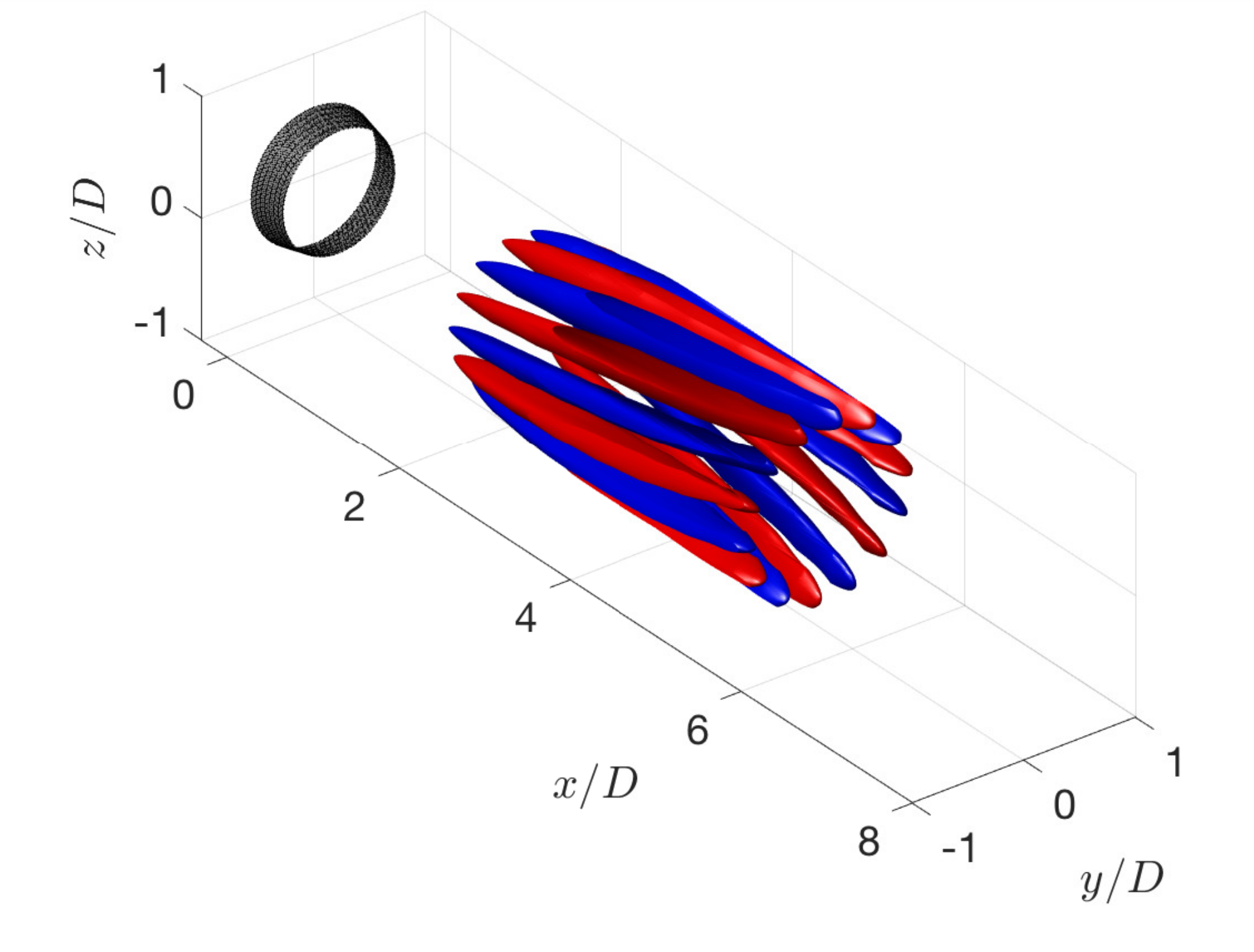
Lift-up, Kelvin–Helmholtz and Orr mechanisms in turbulent jets
E. Pickering, G. Rigas, P. A. S. Nogueira, A. V. G. Cavalieri, O. T. Schmidt, T. Colonius
Journal of Fluid Mechanics 892, A2 (2020)
BIB ABSTRACT
Three amplification mechanisms present in turbulent jets, namely lift-up, Kelvin– Helmholtz and Orr, are characterized via global resolvent analysis and spectral proper orthogonal decomposition (SPOD) over a range of Mach numbers. The lift-up mechanism was recently identified in turbulent jets via local analysis by Nogueira et al. (J. Fluid Mech., vol. 873, 2019, pp. 211–237) at low Strouhal number (St) and non-zero azimuthal wavenumbers (m). In these limits, a global SPOD analysis of data from high-fidelity simulations reveals streamwise vortices and streaks similar to those found in turbulent wall-bounded flows. These structures are in qualitative agreement with the global resolvent analysis, which shows that they are a response to upstream forcing of streamwise vorticity near the nozzle exit. Analysis of mode shapes, component-wise amplitudes and sensitivity analysis distinguishes the three mechanisms and the regions of frequency–wavenumber space where each dominates, finding lift-up to be dominant as St/m → 0. Finally, SPOD and resolvent analyses of localized regions show that the lift-up mechanism is present throughout the jet, with a dominant azimuthal wavenumber inversely proportional to streamwise distance from the nozzle, with streaks of azimuthal wavenumber exceeding five near the nozzle, and wavenumbers one and two most energetic far downstream of the potential core.
-

-
Resolvent-based jet noise models - a projection approach
E. Pickering, A. Towne, P. Jordan, T. Colonius
Proceedings of AIAA Scitech, Orlando 0999 (2020)
BIB ABSTRACT
Linear resolvent analysis has demonstrated encouraging results for modeling coherent structures in jets when compared against their data-deduced counterparts from high-fidelity large-eddy simulations (LES). However, leveraging resolvent modes for reconstructing statistics of the far acoustic field remains elusive. In this study, we use a LES database to produce an ensemble of realizations for the acoustic field that we project on to a limited set of n resolvent modes. The projections are done on a restricted acoustic output domain, r/D = [5, 6], and allow for the LES realizations to be recast in the resolvent basis via a datadeduced, low-rank, n × n cross-spectral density matrix. We find substantial improvements to the acoustic field reconstructions with the addition of a RANS-derived eddy-viscosity model to the resolvent operator. The reconstructions quantitatively match the most energetic regions of the acoustic field across Strouhal numbers, St = [0 − 1], and azimuthal wavenumbers, m = [0, 2], using only three resolvent modes. Finally, the characteristics of the resulting n × n covariance matrices are examined and suggest off-diagonal terms may be neglected for n ≤ 3. Results are presented for round, isothermal, Mach 1.5 and 0.9 jets.
2019
-
-
Eddy viscosity for resolvent-based jet noise models
E. Pickering, G. Rigas, O. T. Schmidt, D. Sipp, T. Colonius
Proceedings of AIAA/CEAS Aeroacoustics, Delft 2454 (2019)
BIB ABSTRACT
Response modes computed via linear resolvent analysis have shown promising results for qualitatively modeling both the hydrodynamic and acoustic fields in jets when compared to data-deduced modes from high-fidelity, large-eddy simulations (LES). For an improved quantitative prediction of the near- and far-field, the role of Reynolds stresses must also be considered. In this study, we propose a methodology to deduce an eddy-viscosity model that optimally captures the nonlinear forcing of resolvent modes. The methodology is based on the maximization of the projection between resolvent analysis and spectral proper orthogonal decomposition (SPOD) modes using a Lagrangian optimization framework. For a Mach 0.4 round, isothermal, turbulent jet, four methods are used to increase the projection coefficients: linear damping, spatially constant eddy-viscosity field, a turbulent kinetic energy derived viscosity field, and an optimized eddy-viscosity field. The resulting projection coefficients for the optimized eddy-viscosity field between SPOD and resolvent can be increased to over 90% for frequencies in the range St = 0.35−1 with significant improvements to St < 0.35. We find that the use of a frequency-independent turbulent kinetic energy turbulent viscosity model produces modes closely inline with optimal results, providing a preliminary eddy-viscosity resolvent model for jets.
-

-
Streaks and coherent structures in jets from round and serrated nozzles
G. Rigas, E. Pickering, O. T. Schmidt, P. A. S. Nogueira, A. V. G. Cavalieri, G. A. Bres, T. Colonius
Proceedings of AIAA/CEAS Aeroacoustics, Delft 2597 (2019)
BIB ABSTRACT
Hydrodynamic instabilities are directly related to large-scale coherent structures that are correlated with jet noise emission. Unravelling and accurately predicting their fundamental dynamics shows a promising direction for designing quieter jet engines. In this study, we analyze high-fidelity large-eddy simulation data of a turbulent Mach 0.4 round jet and a Mach 1.5 chevron jet. Using spectral proper orthogonal decomposition we identify, beyond the well-known Kelvin–Helmholtz and Orr mechanisms, elongated alternating streamwise streaks of high and low-speed fluid that have been associated with a non-modal lift-up effect in wall-bounded shear flows. In the global three-dimensional domain, the most energetic streaks manifest for azimuthal wavenumber m = 1 and frequency St → 0. Furthermore, for the chevron jet, streaks and streamwise vortices appear due to the presence of the serrated nozzle, and they inherit the periodicity of the nozzle geometry. Finally, local (planar) spectral proper orthogonal decomposition is used to analyze the coherent structures of the chevron jet flow. Near the nozzle exit, antisymmetric and symmetric modes appear to be amplified and linked to the presence of the chevrons/streaks. Further downstream, the most energetic modes share similar characteristics to the ones observed in round jets.
-
-
Resolvent-based analysis of streaks in turbulent jets
P. A. S. Nogueira, A. V. G. Cavalieri, O. T. Schmidt, P. Jordan, V. Jaunet, E. Pickering, G. Rigas, T. Colonius
Proceedings of AIAA/CEAS Aeroacoustics, Delft 2569 (2019)
BIB ABSTRACT
Large scale, elongated structures, similar those ones widely studied in wall-bounded flows, are also present in turbulent jets. Several characteristics of these streaks can be identified via reduced order models such as resolvent analysis. The present work involves a resolvent-based study of these structures in turbulent jets. We focus on obtaining the optimal forcing that generates these energetic coherent structures. Results are compared with experimental data post-processed using spectral proper orthogonal decomposition, allowing us to draw conclusions about the nature of the non-linear forcing, since the two analyses should provide equivalent results if this term is modelled as spatially white. By identifying streaks in a global framework, we expect to better understand the mechanism by which they are generated.
2018
-
-
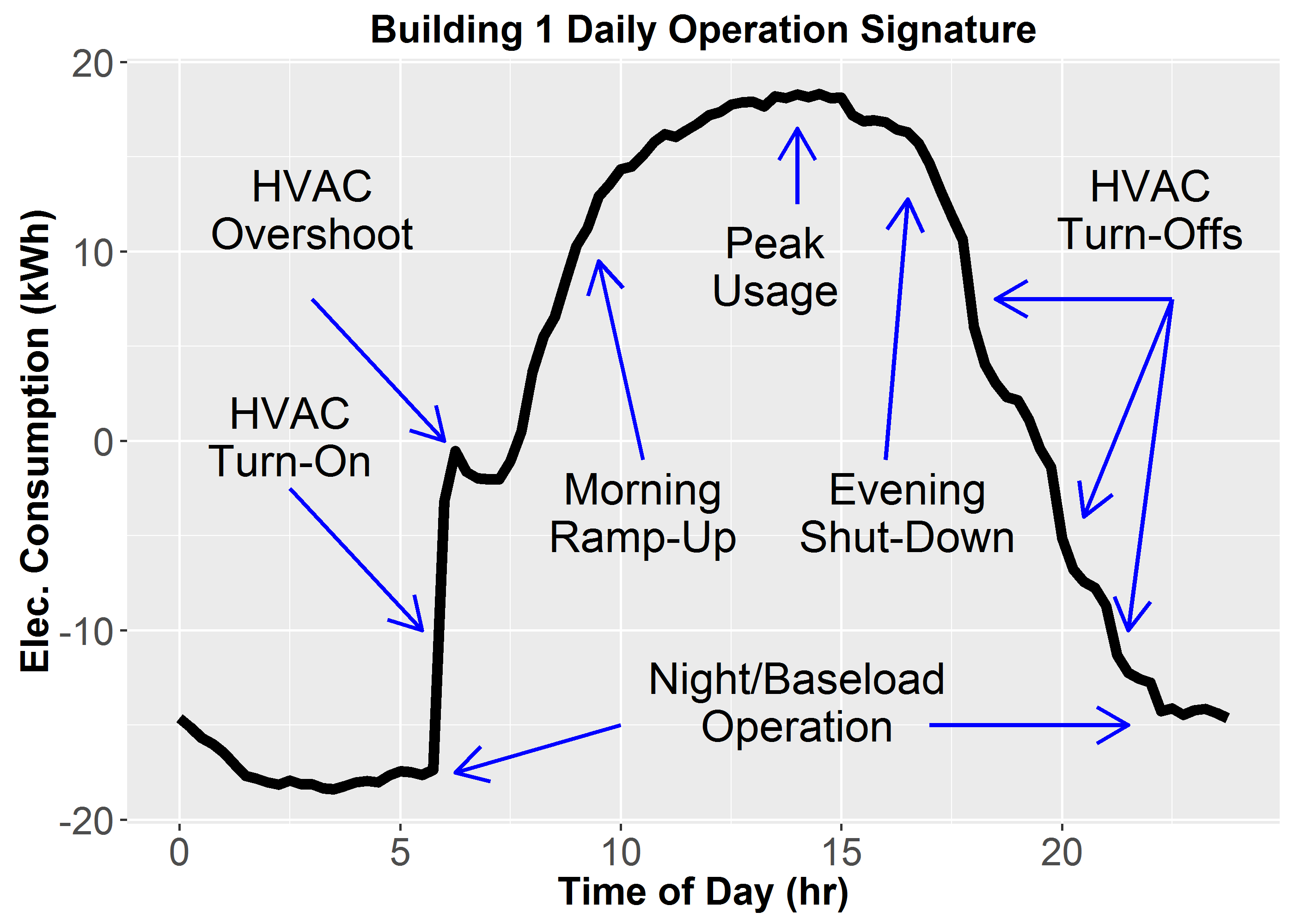
Building electricity consumption - Data analytics of building operations with classical time series decomposition and case based subsetting
E. Pickering, M. A. Hossain, R. H. French, A. R. Abramson
Buildings and Energy 177, 184-196 (2018)
BIB ABSTRACT
The commercial building sector consumes approximately one-fifth of U.S. total energy and exhibits significant operational inefficiencies, leaving a great opportunity to implement various energy-efficiency measures. However, conventional energy audit techniques are expensive, time-consuming, and frequently inaccurate. Conversely, classical time series decomposition of smart meter (i.e. 15 min interval) building electricity consumption provides quick, inexpensive, and useful insights to building operation and characteristics. Paired with complementary time series datasets such as outdoor temperature and solar irradiation, specific insights into HVAC scheduling, daily operational variation, and the relative impact of temperature and solar radiation were quantitatively assessed. This work analyzes six commercial buildings and identifies various building characteristics, including the potential for savings of over 700 MWh valued at 92,000 per year from building rescheduling alone. With access to only whole building smart meter data, these results are obtained virtually and instantaneously, making the case for a rigorous data analytics approach to unlock the potential of building energy efficiency.
2017
-
A cross-sectional study of the temporal evolution of electricity consumption of six commercial buildings
E. Pickering, M. A. Hossain, J. P. Mousseau, R. A. Swanson, R. H. French, A. R. Abramson
PLOS One (2017)
BIB ABSTRACT
Current approaches to building efficiency diagnoses include conventional energy audit techniques that can be expensive and time consuming. In contrast, virtual energy audits of readily available 15-minute-interval building electricity consumption are being explored to provide quick, inexpensive, and useful insights into building operation characteristics. A cross sectional analysis of six buildings in two different climate zones provides methods for data cleaning, population-based building comparisons, and relationships (correlations) of weather and electricity consumption. Data cleaning methods have been developed to categorize and appropriately filter or correct anomalous data including outliers, missing data, and erroneous values (resulting in < 0.5 percent anomalies). The utility of a cross-sectional analysis of a sample set of building’s electricity consumption is found through comparisons of baseload, daily consumption variance, and energy use intensity. Correlations of weather and electricity consumption 15-minute interval datasets show important relationships for the heating and cooling seasons using computed correlations of a Time-Specific-Averaged-Ordered Variable (exterior temperature) and corresponding averaged variables (electricity consumption)(TSAOV method). The TSAOV method is unique as it introduces time of day as a third variable while also minimizing randomness in both correlated variables through averaging. This study found that many of the pair-wise linear correlation analyses lacked strong relationships, prompting the development of the new TSAOV method to uncover the causal relationship between electricity and weather. We conclude that a combination of varied HVAC system operations, building thermal mass, plug load use, and building set point temperatures are likely responsible for the poor correlations in the prior studies, while the correlation of time-specific-averaged-ordered temperature and corresponding averaged variables method developed herein adequately accounts for these issues and enables discovery of strong linear pair-wise correlation R values. TSAOV correlations lay the foundation for a new approach to building studies, that mitigates plug load interferences and identifies more accurate insights into weather-energy relationship for all building types. Over all six buildings analyzed the TSAOV method reported very significant average correlations per building of 0.94 to 0.82 in magnitude. Our rigorous statistics-based methods applied to 15-minute-interval electricity data further enables virtual energy audits of buildings to quickly and inexpensively inform energy savings measures.
2016
-
EDIFES 0.4 - Scalable data analytics for commercial building virtual energy audits
E. Pickering
Master's Thesis (2016)
BIB ABSTRACT
Energy Diagnostics Investigator for Efficiency Savings (EDIFES) has been developed for scalable data analytics to conduct virtual energy audits on commercial buildings. Built as a software package in R, EDIFES ingests building electricity data and readily available weather data, applying various data analytics to determine building markers, characteristics, and operational tendencies. Through these analyses building systems are identified, including Heating Ventilation and Air Conditioning (HVAC), lighting, and plug load or other equipment, with characteristics such as load and system scheduling. Once building systems have been identified, EDIFES conducts virtual energy audits to diagnose efficiency issues, determines the impact (i.e. return-on-investment or payback) of potential retrofit actions (e.g. reschedulingHVAC to occupied hours or conducting a lighting retrofit). After this stage, it can be used for measurement and verification (M&V) or continuous commissioning. Six buildings are presented in this thesis.